



b. 29 April 1667, Arbuthnot, Kinkardineshire, Scotland
d. 27 February 1735, London, England
John Arbuthnot studied at Aberdeen, Scotland and earned a doctor of medicine degree from St. Andrews in 1696.
He was elected to the Royal Society in 1704, became physician extraordinary to Queen Anne in 1704, physician ordinary in 1709, and fellow of the Royal College of Physicians in 1710.
| "All those Problems suppose Chances, which are in an equal probability to happen, if it should be suppos'd otherwise, there will arise variety of Cases of a quite different nature, which, perhaps, 'twere'not unpleasant to consider, I shall add one Problem of that kind, leaving the Solution to those who think it merits their pains. In Parallelipipedo cujus latera sunt ad invicem in ratione a, b, c: Invenire quotâ vie quivis suscipere potest, ut datum quodvis planum, v. g. ab jaciat.'' |
Arbuthnot is most famous for his short paper “An Argument for Divine Providence, Taken from the Constant Regularity Observ'd in the Birth of Both Sexes.” which appeared in the Philosophical Transactions 27 published in 1710. See also the response to this by 'sGravesande.
The paper contains a table of the number of christenings in London by sex of the child for the years 1629 to 1710 inclusive. What Arbuthnot finds extraordinary is the apparent regularity in the ratio of births. This can be seen quite clearly in the graph below. Here 1629 is year 1.
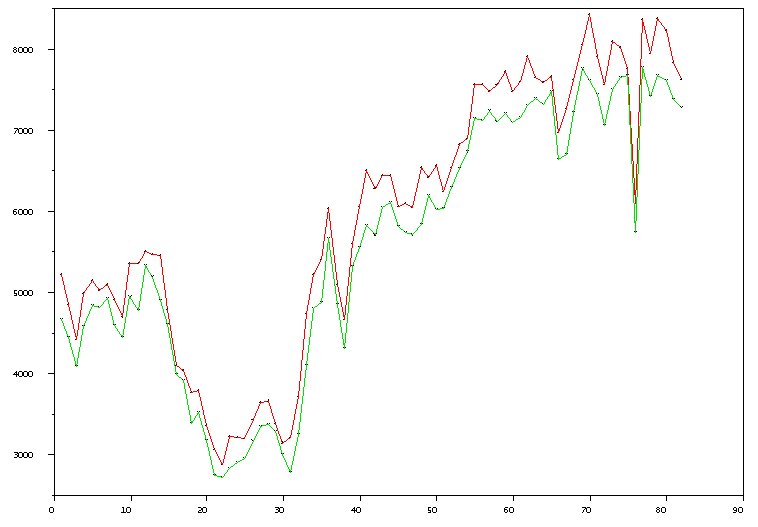 |
The line representing males always lies above the line for females and the two lines move in lockstep. Arbuthnot thought this extraordinary.
Taking an exact balance between the number of male and female births as given, Arbuthnot assumes males and females are born in ratio 1:1. Arbuthnot first asks how likely it is that the same number of males as females be born when there are thousands upon thousands of births. To this question he finds that as the number of births increase, the chance this occur decreases to 0.
He next observes that the probability the number of male births exceed the number of female births if they occur in this same ratio can be assumed to be at most 1/2. Therefore, in the span of 82 years, the probability that the number of males exceed the number of females each and every time cannot exceed 1/282, an extremely small number. This is morally impossible.
What does this conclusion mean to Arbuthnot? He does not reject the hypothesis that births are in 1:1 ratio. Because males have a greater mortality, if every woman is to have a mate, more males must be born than females. More males are born because of Divine Design. This can only be due by Art, not Chance.
One may consult E. Shoesmith, "The continental controversy over Arbuthnot's argument for Divine providence," Historia Mathematica 14 (1987), pp. 133-146.