Mémoire sur les suites récurro-récurrentes
et sur leur usages dans la théorie des hasards

PROBLEM V . — If in a pile of x pieces one takes a number at random, it is necessary to determine the probability that this number be even or odd .

Let y denote the sum of the even cases, z the sum of the odd. Laplace observes the two equations relating the quantities.

> eqn1:=y(x+1)=y(x)+z(x);

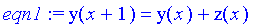
> eqn2:=z(x+1)=z(x)+y(x)+1;

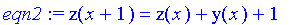
If there is but 1 piece ( 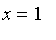), then the sum of the odd must be 1. Therefore, the particular solution is given by

> sol:=rsolve({eqn1,eqn2,y(1)=0,z(1)=1},{y,z});

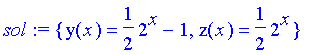
Clearly, odds are favored over evens. Now, if we compute the total number of cases: t(x)=y(x)+z(x), we can compute the probabilities of each. Namely,

> t:=rhs(sol[1]+sol[2]);

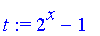
> prob_even:=unapply(rhs(sol[1])/t,x);

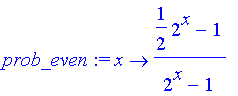
> prob_odd:=unapply(rhs(sol[2])/t,x);

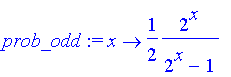
For example, if we let 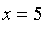we obtain the odds

> prob_even(5)/prob_odd(5);

>
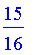